Parábola
 |
Si das una patada a una pelota de fútbol (o disparas una flecha o un misil, o tiras una piedra) seguirá un arco en el aire y caerá de vuelta...
... ¡siguiendo una parábola!
(Excepto por el efecto del aire.)
|
Definición
Una parábola es una curva en la que los puntos están ala misma distancia de:
| 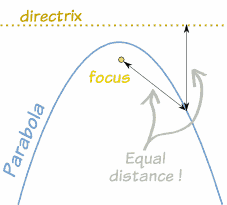 |
En una hoja de papel, dibuja una línea recta, y marca un punto gordo para el foco (¡que no esté en la línea!).
Ahora juega un poco midiendo con una regla hasta que encuentres un punto que esté a la misma distancia del foco y de la línea.
Repite hasta que tengas muchos puntos, uniéndolos tendrás una parábola.
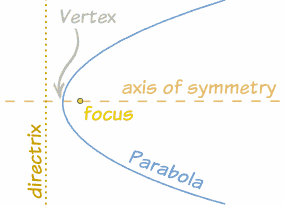 | Nombres
Estos son los nombres más importantes:
|
Reflector
Y la parábola tiene la siguiente propiedad sorprendente:
Un rayo paralelo al eje de simetría se refleja en la superficie directamente hacia el foco.
Así las parábolas se pueden usar para:
| 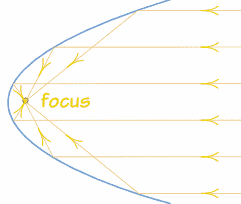 |
| Y por eso el punto central se llama foco... ¡porque ahí es donde se enfocan todos los rayos! |  |
 |
También sale una parábola cuando seccionas un cono (el corte tiene que ser paralelo al lado del cono).
Por tanto, la parábola es una sección cónica (una sección de un cono).
|
Ecuaciones
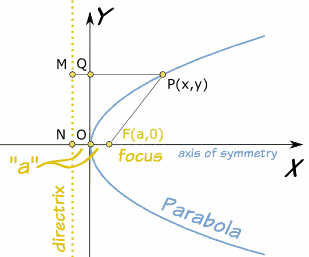
Si pones la parábola en coordenadas cartesianas (gráfico x-y) con:
entonces la curva queda definida por la ecuación:
y2 = 4ax
|  |
Ejemplo: ¿dónde está el foco de la ecuación y2=5x ?
Si ponemos y2 = 5x en la forma y2 = 4ax, tenemos que y2 = 4 (5/4) x,
así que a = 5/4, y el foco de y2=5x es:
F = (a,0) = (5/4,0)
Las ecuaciones de las parábolas en las distintas orientaciones son:
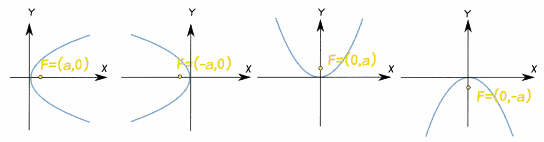 | |||
| y2 = 4ax | y2 = -4ax | x2 = 4ay | x2 = -4ay |
Medidas para una antena parabólica
Si quieres construir una antena parabólica que tenga el foco 200 mm sobre la superficie, ¿qué medidas necesitas?
Para que sea fácil de hacer, digamos que apunte hacia arriba, y así tenemos la ecuación x2 = 4ay.
Y queremos que "a" sea 200, así que la ecuación queda:
x2 = 4ay = 4 × 200 × y = 800y
Lo reescribimos para poder calcular las alturas:
y = x2/800
Aquí tienes algunas medidas de alturas que van saliendo:
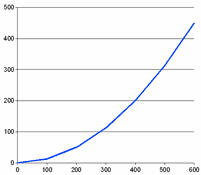 | Distancia horizontal ("x") | Altura ("y") |
| 0 mm | 0.0 mm | |
| 100 mm | 12.5 mm | |
| 200 mm | 50.0 mm | |
| 300 mm | 112.5 mm | |
| 400 mm | 200.0 mm | |
| 500 mm | 312.5 mm | |
| 600 mm | 450.0 mm | |
Elipse
Una elipse es una circunferencia aplastada.
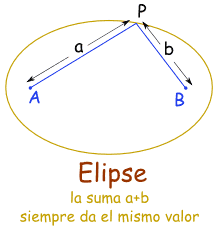
Una circunferencia tiene un centro, pero una elipse tiene dos focos ("A" y "B" abajo).
Definición
Una elipse es el conjunto de todos los puntos de un plano cuya
suma de distancias a dos puntos fijos es una constante.
Así que, no importa dónde estés en la elipse, puedes sumar las distancias al punto "A" y al punto "B" y siempre saldrá lo mismo.
(Los puntos "A" y "B" se llaman los focos de la elipse)
|  |
Dibújala
Clava dos clavos en un tablero, pon un lazo de cuerda alrededor de ellos, y pon un lápiz en el lazo. Tensa la cuerda para que forme un triángulo, y sigue la línea... habrás dibujado una elipse.
Una circunferencia es una elipse
En realidad una circunferencia es una elipse, donde los dos focos son el mismo punto (el centro). O sea, una circunferencia es un "caso especial" de elipse.
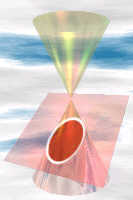 | Sección de un cono
También sale una elipse cuando cortas un cono (con un ángulo pequeño).
Por tanto, la elipse es una sección cónica (una sección de un cono).
|
Calculando
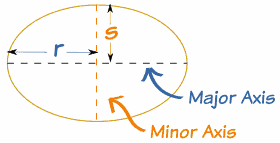 | Área
El área de una elipse es π × r × s
(Si es una circunferencia, r y s son iguales, y sale π × r × r = πr2, ¡que es correcto!)
|
Aproximación al perímetro
Aunque parezca extraño, el perímetro de una elipse es muy difícil de calcular, así que he creado una página especial para ese tema: lee Perímetro de una elipse para ver los detalles.
Pero una aproximación sencilla que está a menos de 5% del valor correcto (siempre que r no sea más de 3 veces s) es la siguiente:
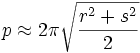
No hay comentarios:
Publicar un comentario