Simplificación de ecuaciones trigonometricas

Para simplificar expresiones trigonométricas utilizamos las mismas técnicas empleadas empleadas para simplificar expresiones algebraicas y las identidades trigonométricas fundamentales.

Ejemplos:

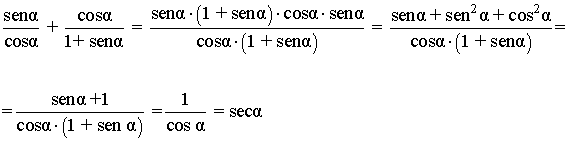
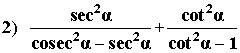
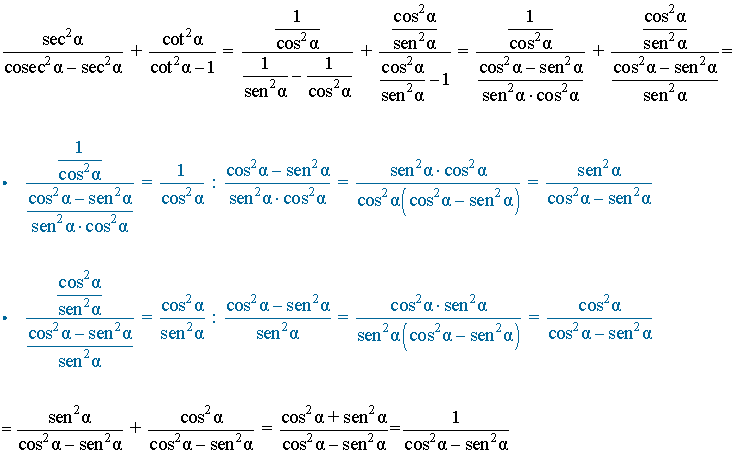
VERIFICACION DE EXPRESIONES TRIGONOMETRICAS – DEMOSTRACION DE IDENTIDADES.

Verificar una identidad trigonométrica consiste en demostrar que efectivamente ambos lados de la igualdad son equivalentes. Usaremos operaciones algebraicas e identidades trigonométricas conocidas para convertir uno de los lados de la ecuación exactamente en la forma en que está expresado el otro lado de la ecuación.

Ejemplo 1:

Verificar:	$$\frac{}{}$$ 2 ( x ) -1 sec 2 ( x ) = sen 2 ( x )
Solución:
Partiendo del lado izquierdo de la ecuación	$$\frac{}{}$$ 2 ( x ) -1 sec 2 ( x )
Reescribiendo sec(x) en términos de coseno	$$\frac{}{}$$ cos2 x - 1 1 cos2 x
	$$\frac{}{}$$ - cos 2 x cos 2 x 1 cos 2 x
	$$\frac{}{}$$ - cos 2 x cos 2 x 1 cos 2 x
Simplificando	$$1$$ - cos 2 x
Usando la identidad $cos$ 2 ( α ) + sen 2 ( α ) = 1	$$cos$$ 2 ( α ) + sen 2 ( α ) - cos 2 x
Simplificando obtenemos el lado derecho de la ecuación	$${\mathrm{sen}}^{}$$ 2 x

---

Ejemplo 2:

Verificar:	$$\frac{}{}$$ 1- sen ( x ) + 1 1+ sen ( x ) = 2 sec 2 ( x )
Solución:
Partiendo del lado izquierdo de la ecuación	$$\frac{}{}$$ 1- sen ( x ) + 1 1+ sen ( x )
Combinando las fracciones	$$\frac{}{}$$ + sen ( x ) + 1 - sen ( x ) 1 - sen ( x ) 1 + sen ( x )
Simplificando	$$\frac{}{}$$ 1 - sen2 ( x )
Usando la identidad $cos$ 2 ( α ) + sen 2 ( α ) = 1	$$\frac{}{}$$ cos 2 ( α ) + sen 2 ( α ) - sen2 ( x )
Simplificando	$$\frac{}{}$$ cos 2 ( x )
Usando la definición de sec(x) obtenemos el lado derecho de la ecuación	$$2$$ sec 2 ( x )