Identidades para ángulos dobles y medios.

Ángulo doble

Fórmulas del ángulo doble

Fórmulas para reducir la potencia

De las identidades de $cos$ ( 2 x ) podemos deducir:

$sen$ 2 ( x ) = 1 − cos ( 2 x ) 2

$cos$ 2 ( x ) = 1 + cos ( 2 x )2

$tan$ 2 ( x ) = 1 − cos ( 2 x ) 1+ cos ( 2 x )

Ejemplos:

1. Encontrar sen(2x) y cos(2x) dada la información: sec(x)=2 y x está en el cuadrante IV.

Solución:

a. De la definición de la función secante sabemos que: $sec$ (x) = 1 cos (x) , entonces podemos hallar fácilmente cos(x):
$1$ cos (x) =2 , por lo tanto despejando obtenemos: $cos$ (x) = 1 2

Por la identidad de pitágoras sabemos que: $sen$ (x) = − 1 − cos 2 (x) , se utiliza la raíz negativa ya que x está en el cuarto cuadrante. Con esta fórmula podemos hallar fácilmente sen(x):

$sen$ ( x ) = − 1 − ( 1 2 ) 2 = − 1 − 1 4 = − 3 4 = − 3 2

De las fórmulas antes mostradas sabemos que $sen$ ( 2 x ) = 2 sen ( x ) cos ( x ) , entonces:

$sen$ ( 2 x ) = 2 − ( − 3 2 ) 1 2 = − 3 2

igualmente sabemos que $cos$ ( 2 x ) = cos 2 ( x ) − sen 2 ( x ) , entonces:

$cos$ ( 2 x ) = ( 1 2 ) 2 − ( − 3 2 ) 2 = 1 4 − 3 4 = − 2 4 = − 1 2

2. Usar las identidades para reducir la potencia, reescribiendo la expresión en términos de la primera potencia de coseno: 

     $$ cos 2 ( x ) sen 2 ( x )

Solución:

$cos$ 2 ( x ) sen 2 ( x ) = ( 1 + cos ( 2 x ) 2 ) ( 1 − cos ( 2 x ) 2 ) = 1 − cos 2 ( 2 x ) 4 = ( 1 4 − cos 2 ( 2 x ) 4 ) = 1 4 − 1 4 ( 1 + cos ( 4 x ) 2 ) = 1 4 − ( 1 +cos ( 4 x ) ) 8 = 2 − 1 − cos ( 4 x ) 8 = 1 − cos ( 4 x ) 8

3. Reescribir $sen$ 4 ( x ) como una suma de primeras potencias de coseno.

Solución:

$sen$ 4 ( x ) = ( sen 2 ( x ) ) 2 = ( 1 − cos ( 2x ) 2 ) 2 = 1 4 ( 1 − 2 cos ( 2 x ) + cos 2 ( 2 x ) ) = 1 4 ( 1 − 2 cos ( 2 x ) + ( 1 + cos ( 4 x ) 2 ) ) = 1 4 − 1 2 cos( 2 x ) + 1 8 ( 1 + cos ( 4 x ) ) = 2 − 4 cos ( 2 x ) + 1 + cos ( 4 x ) 8 = 1 8 ( 3 − 4 cos ( 2 x ) + cos ( 4 x ) )

4. Considera la gráfica siguiente de la función $f$ ( x ) = 4 cos 2 ( x ) − 2

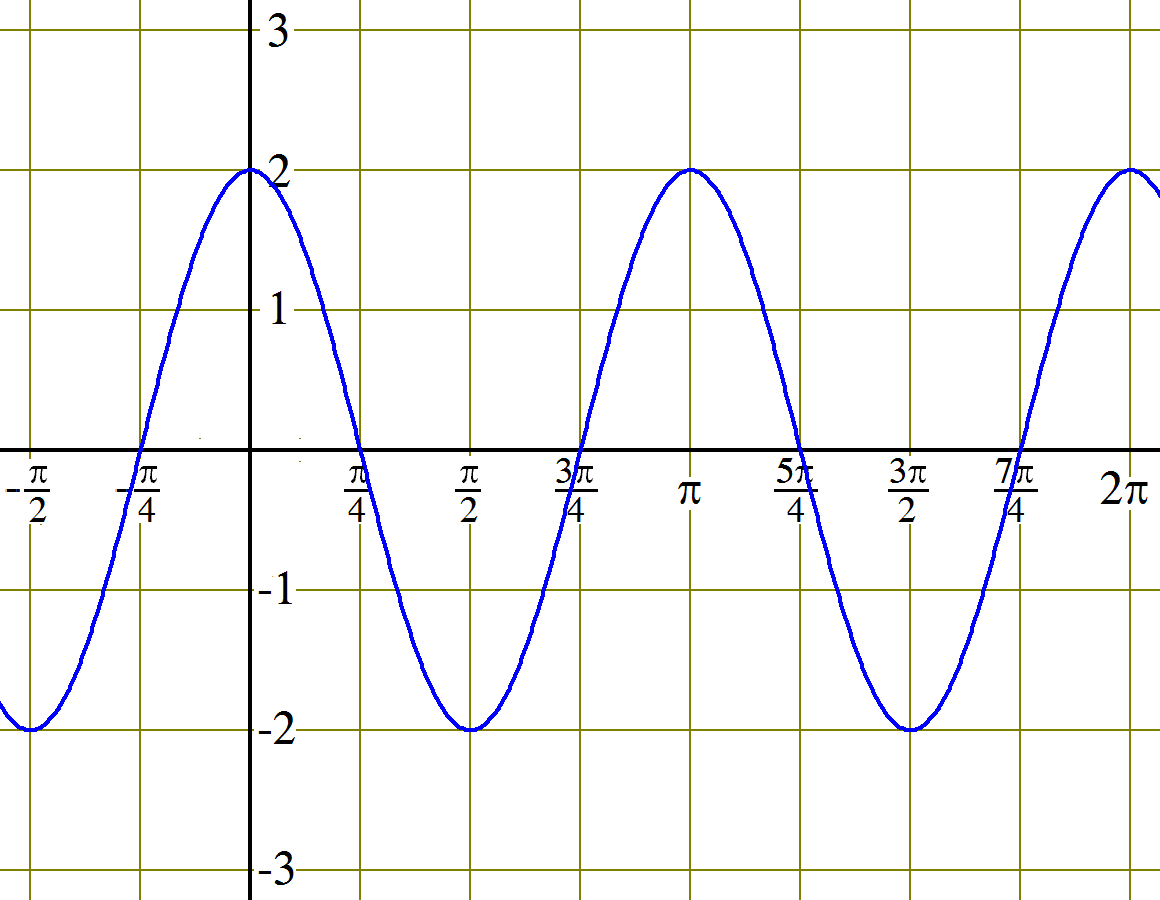
Se parece mucho a una transformación de la gráfica de coseno. Si la gráfica es una transformación de la de coseno, ¿cuál podría ser? ¿Cómo se demuestra que la función original y la transformación de coseno que aparenta ser son iguales de verdad?

Solución:

Primero, mirando la gráfica como fuera una transformación de coseno, en seguido se ve que tiene amplitud 2, periodo π, desplazamiento vertical 0 y desfase (desplazamiento horizontal) 0.

Si $f$ ( x ) = 4 cos 2 ( x ) − 2 es equivalente a una transformación de cos(x), tiene que ser igual a 2cos(2x).

Ahora utilizamos las identidades de doble ángulo que tenemos:

     $$ 4 cos 2 ( x ) − 2 = 4 ( 1 + cos ( 2 x ) 2 ) − 2

                 $$ = 2 + 2 cos ( 2 x ) − 2

                 $$ = 2 cos ( 2 x )

Después de todo fue facil mostrar que las dos funciones tienen que ser iguales. Primero tuvimos que dar cuenta que podrian ser iguales. En eso examinar la gráfica nos llevo a sospechar que se podria expresar de otra forma.

5. Expresar sen(3x) en términos de sen(x).

$sen$ ( 3 x ) = sen ( 2 x + x ) = sen ( 2 x ) cos ( x ) + cos ( 2 x ) sen ( x ) = 2 sen ( x ) cos ( x ) cos ( x ) + ( 1 − 2 sen 2 ( x ) ) sen ( x ) = 2 sen ( x ) cos 2 ( x) + sen ( x ) − 2 sen 3 ( x ) = 2 sen ( x ) ( 1 − sen 2 ( x ) ) + sen ( x ) − 2 sen 3 ( x ) = 2 sen ( x ) − 2 sen 3 ( x ) + sen ( x ) − 2 sen 3 ( x ) = 3 sen ( x ) − 4sen 3 ( x )

Fórmulas del ángulo medio

Fórmulas del ángulo mitad

Ejemplos:

1. Hallar el valor exacto de $sen$ ( 5π 6 )

Solución:

$5\pi$ 6 está en el I cuadrante, entonces elegimos el signo positivo (+)

$sen$ ( 5π 6 ) = 1 − cos ( 5π 6 ) 2 = 1 − ( − cos ( 5π 6 ) ) 2 = 1 + 3 2 2 = 2 + 3 2 2 = 2 + 3 4

2. Hallar el valor exacto de sen(22.5°)

Solución:

Como 22.5° es la mitad de 45°, el ángulo se encuentra en el primer cuadrante por lo tanto la función seno tiene signo positivo.

$sen$ ( 45° 2 ) = 1 − cos ( 45° ) 2 = 1 − 2 2 2 = 2 − 2 4 = 1 2 ( 2 − 2 )

3. Encontrar $sen$ ( x 2 ) si $cos$ ( x ) = − 4 5   y   180° < x < 270°.

Solución:

Ya que 180° < x < 270°, entonces x está en el tercer cuadrante y por lo tanto $x$ 2 está en el segundo cuadrante. Entonces el signo de la función seno será positivo.
$sen$ ( x 2 ) = 1 − ( cos x ) 2 = 1 + 4 5 2 = 5 + 4 10 = 9 10 = 3 10 10